When planning a path toward biostatistics, students often face a critical decision between advanced mathematical courses: Calculus 2 versus Linear Algebra. Both subjects form essential foundations for statistical modeling and data analysis, yet each contributes uniquely to biostatistical applications. This guide examines their respective values and provides framework for making an informed choice.
Core Mathematical Requirements in Biostatistics
Biostatistics programs typically require proficiency in three key areas:
- Probability theory (built upon calculus foundations)
- Statistical modeling (requiring matrix operations from linear algebra)
- Computational methods (combining both disciplines)
According to American Statistical Association guidelines, graduate programs expect applicants to demonstrate competence in multivariate calculus and matrix algebra. However, course sequencing often depends on individual program structures.
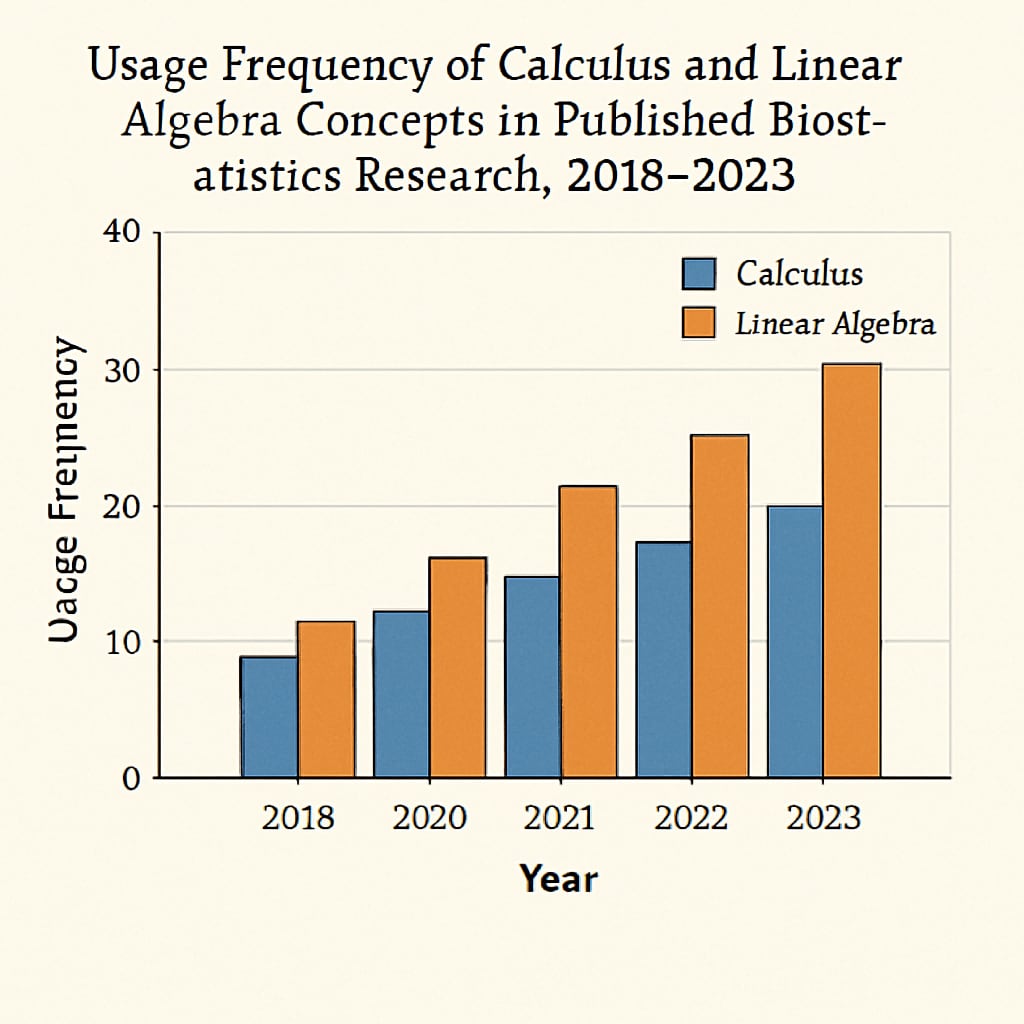
Strategic Course Selection Approaches
Consider these four decision factors when choosing between the courses:
- Program prerequisites: Check requirements of target graduate schools
- Career specialization: Machine learning emphasizes linear algebra; epidemiological modeling uses more calculus
- Course availability: Some universities offer biostatistics-focused linear algebra versions
- Personal proficiency: Assess which mathematical thinking comes more naturally
A National Institutes of Health study found that students taking linear algebra before graduate school adapted faster to modern biostatistics coursework.
Complementary Learning Solutions
For students unable to take both courses before graduation, consider these alternatives:
- Summer intensive programs at research universities
- Verified online courses with computational applications
- Undergraduate research projects applying both disciplines
Many institutions now offer Applied Linear Algebra for Statistics courses specifically designed for future data scientists.

Readability guidance: Key concepts are explained using relatable examples from public health research. Transition words like “however” and “therefore” connect analytical points, while bullet lists break down complex recommendations.


