Introduction
Preparing for the AMC 8 can feel challenging, but working through AMC 8 real questions with detailed solutions is one of the best ways to improve problem-solving skills. In this article, we analyze selected past problems, break down the key math concepts, and share strategies that help students succeed in the AMC 8 and beyond.
In this article, we analyze three representative AMC 8 real questions from 2025 contest—Problem 15 (combinatorics), Problem 18 (geometry), and Problem 22 (number theory). Each problem highlights common challenges and strategies for success.
AMC 8 Real Question 1 — Combinatorics (Grid Folding with Colors)
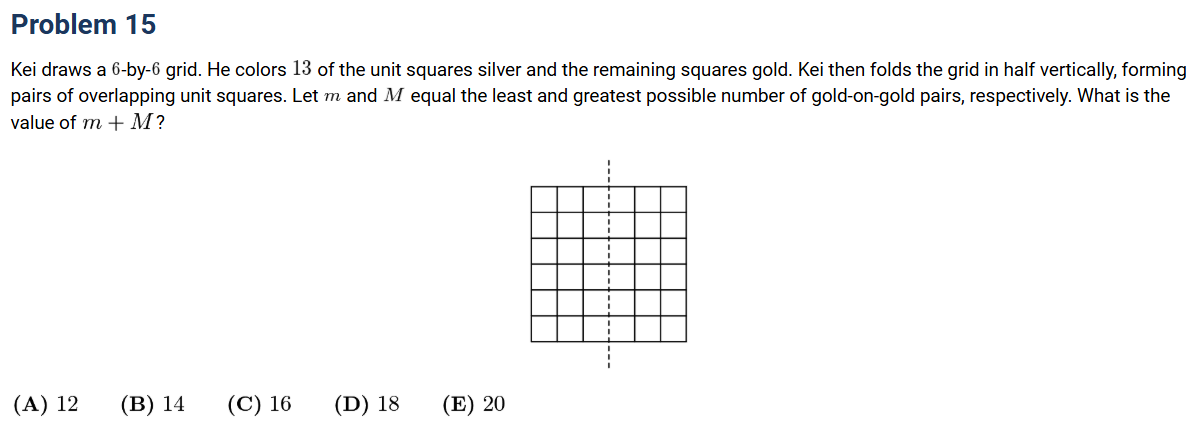
Question Recap:
A 6×6 grid is colored with 13 silver squares and the remaining squares gold. When the grid is folded vertically, pairs of overlapping unit squares are formed. Students must determine the minimum (m) and maximum (M) number of gold-on-gold pairs, then calculate m + M.
Key Skills Tested:
- Counting techniques
- Combinatorics and case analysis
- Logical reasoning with symmetry
Why It’s Tricky:
The problem requires students to visualize folding and overlapping, which combines spatial reasoning with combinatorial counting. Many students miscount pairs or overlook edge cases.
Solution Outline:
- Total pairs after folding: 18 pairs (since 6×6 grid folded in half gives 18 overlapping pairs).
- Analyze the placement of silver vs. gold squares.
- Find minimum and maximum possible gold-on-gold pairs.
- Result: m+M=16m+M = 16m+M=16.
AMC 8 Real Question 2 — Geometry (Circle and Inscribed Square)
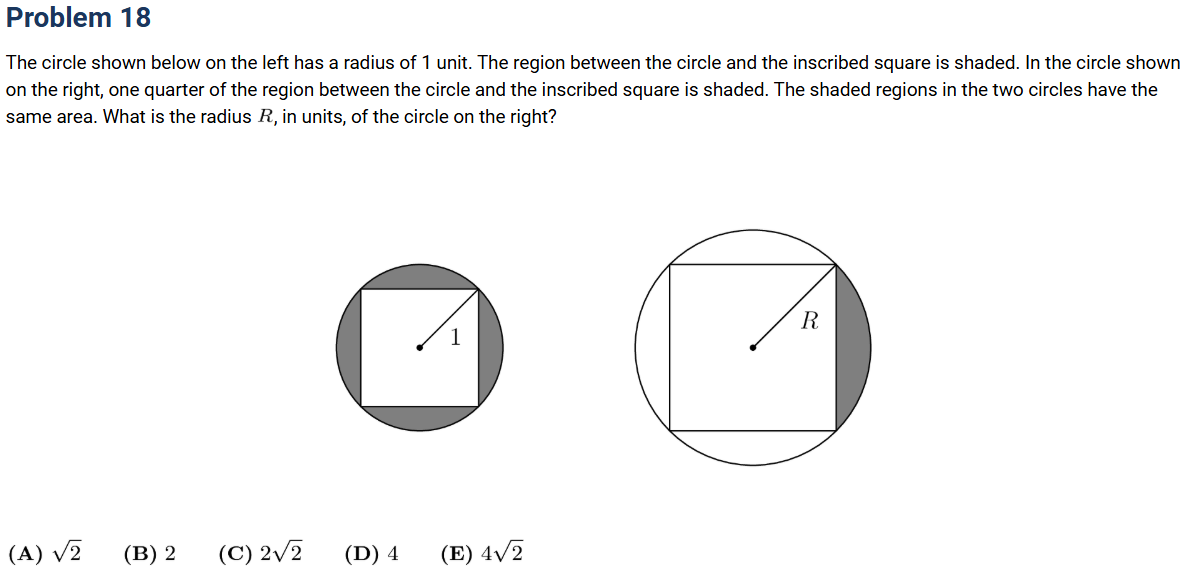
Question Recap:
A circle with radius 1 has a shaded region between the circle and its inscribed square. Another larger circle with radius R has one-quarter of that same type of shaded region. Students must solve for R.
Key Skills Tested:
- Area of circles and squares
- Geometric reasoning with proportions
- Algebraic manipulation
Why It’s Tricky:
This problem tests multi-step reasoning. Students must calculate the shaded area using πr2−s2\pi r^2 – s^2πr2−s2, then apply proportionality to solve for R.
Solution Outline:
- Small circle shaded area = π(12)−(2)2=π−2\pi(1^2) – (\sqrt{2})^2 = \pi – 2π(12)−(2)2=π−2.
- Larger circle shaded area = 14(πR2−2R2)\frac{1}{4}(\pi R^2 – 2R^2)41(πR2−2R2).
- Equating the two areas gives R=2R = 2R=2.
Answer: (B) 2
AMC 8 Real Question 3 — Number Theory (Coat Hook Spacing)
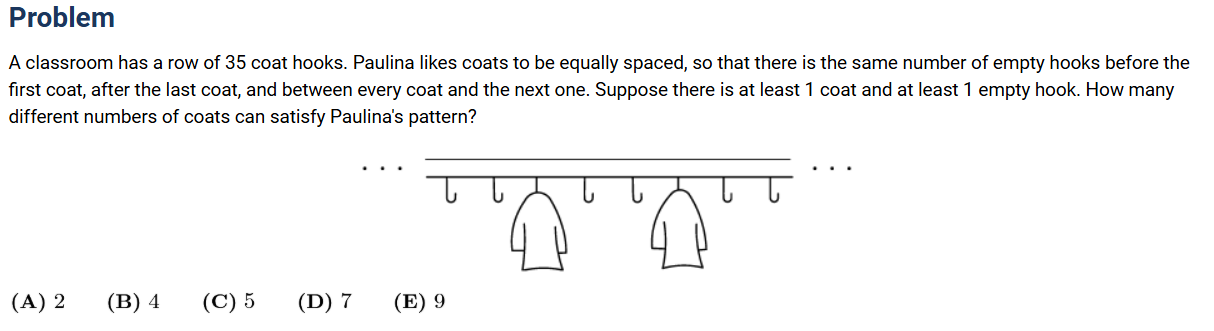
Question Recap:
A classroom has 35 coat hooks. Coats must be equally spaced with at least 1 coat and 1 empty hook. How many different numbers of coats are possible?
Key Skills Tested:
- Divisors and factors
- Number theory applications
- Logical reasoning with real-life models
Why It’s Tricky:
This problem blends real-world modeling with number theory. Students must realize that the number of coats corresponds to the number of divisors of 36 (35 hooks + 1).
Solution Outline:
- Add 1 to 35 hooks → 36 positions.
- Number of coats = divisors of 36.
- Exclude trivial cases (all coats or all empty).
- Valid divisors = 2, 3, 4, 6, 9 → 5 possible answers.
Answer: (C) 5
What We Learn from AMC 8 2025
- Geometry (36%) remains the heaviest tested category, especially inscribed figures.
- Number Theory (20%) continues to challenge students with factorization and modular reasoning.
- Combinatorics (8%) is smaller in percentage but often requires creative problem-solving.
Together, these problems show why AMC 8 is more challenging than curriculum-based contests like the Gauss math contest.
How Canadian Students Can Prepare
At Think Academy Canada, our structured courses guide students step by step:
- L4 (Grades 4–6): Build strong foundations in fractions, averages, and word problems.
- L5 (Grades 6–7): Prepare for AMC 8 with contest-style geometry, number theory, and combinatorics.
- L6 (Grades 7–8): Transition to AMC 10 and Waterloo contests (Pascal, Cayley, Fermat).
Preparation Tips:
- Practice with past AMC 8 papers under timed conditions.
- Strengthen weak areas (fractions, divisors, geometry).
- Focus on reading comprehension in word problems to avoid misinterpretation.
Preparation with AMC 8 real questions is not just about solving problems — it builds analytical skills, international recognition, and private school application strength.
Ready to take your child’s preparation to the next level?
Join Think Academy Canada’s AMC 8 Prep Programs and give them the tools to succeed.


