Introduction
AMC 8 Counting and Probability is a major topic in the contest and often challenges students who are not yet confident with formulas. These questions include everything from basic counting principles to advanced probability word problems and permutations and combinations. In this guide, we explain the essential rules, show how they work, and highlight AMC 8 past problems that demonstrate each formula. Practicing with worksheets and real contest examples will help students strengthen their problem-solving skills.
This article focuses on AMC 8 Counting and Probability. For a full study plan, also check out our guides on AMC 8 Algebra Formulas and AMC 8 Geometry Formula
1. Sum Rule (Additional Principle)

AMC 8 Example (2015, Problem 4):

The Centerville Middle School chess team has 2 boys and 3 girls. A photographer wants them in a row with a boy at each end and the girls in the middle.
- Case 1: Boy A left, Boy B right → 3!=63! = 63!=6 ways
- Case 2: Boy B left, Boy A right → 3!=63! = 63!=6 ways
- Total = 6+6=126 + 6 = 126+6=12
This is a straightforward AMC 8 counting problem where the Sum Rule is applied by splitting cases and adding the results.
2. Product Rule (Multiplication Principle)
When a process has independent steps, the total number of ways is:

AMC 8 Example (2019, Problem 14):

Isabella redeems coupons every 10 days. Pete’s shop is closed on Sundays. After circling six redemption days, none lands on Sunday. What day of the week did she start?
- Each step shifts 3 days forward (10≡3(mod7)10 \equiv 3 \pmod{7}10≡3(mod7))
- Sequence cycles: Start → +3 → +6 → +2 → +5 → +1
- Only Tuesday avoids Sunday
This is a classic AMC 8 probability word problem that combines modular arithmetic with the Product Rule.
3. Properties of Probability

AMC 8 Example (2016, Problem 21):

A box has 3 red chips and 2 green chips. Chips are drawn without replacement until either all 3 reds or both greens appear. What is the probability that all reds are drawn?
- Success happens if the 3rd red comes before the 2nd green
- Probability = 3/5
Students practicing with probability worksheets will often see problems like this, which test their understanding of basic probability rules.
4. Permutation and Combination

AMC 8 Example (2018, Problem 16):

Professor Chang has 9 books: 2 Arabic, 3 German, 4 Spanish. Arabic must stay together, and Spanish must stay together.
- Treat Arabic and Spanish each as a single block → 7 objects
- Arrange 7 blocks: 7!7!7!
- Internal arrangements: 2!×4!2! \times 4!2!×4!
- Total = 2880
This is a good example of AMC 8 permutations and combinations problems, where grouping restrictions make the problem more challenging.
5. Basic Probability Formulas
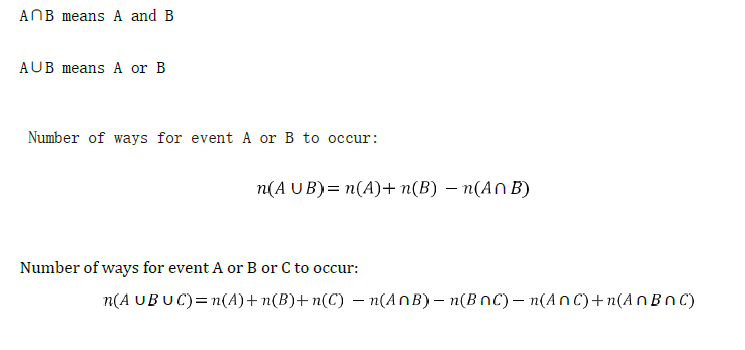
AMC 8 Example (2014, Problem 16):

The “Middle School Eight” basketball conference has 8 teams. Each team plays every other twice plus 4 extra non-conference games.
- Internal games: (82)×2=56{8 \choose 2} \times 2 = 56(28)×2=56
- Non-conference games: 8×4=328 \times 4 = 328×4=32
- Total = 88
This type of AMC 8 probability problem is solved by applying union/intersection-style counting formulas.
Why Practice Matters
Every year, AMC 8 includes multiple counting and probability problems. Some are simple case counts, while others test advanced applications of permutations, combinations, or union/intersection formulas. By practicing with AMC 8 probability worksheets and word problems, students can master these formulas and avoid common traps.
Call to Action
At Think Academy Canada, our AMC 8 program helps students:
- Understand counting and probability formulas in depth
- Practice with worksheets and past AMC 8 problems
- Build skills step by step for contests like AMC 10 and Waterloo Gauss
Take a free evaluation and learn more about our AMC 8 courses here.


