Introduction
Sudoku is one of the world’s most popular logic puzzles. Parents and students often ask: “Can playing Sudoku actually help with math contest preparation, especially for the Gauss Math Contest, Waterloo Math Competition, or even Math Kangaroo Canada?”
The short answer is yes—but with limits. While Sudoku does not teach algebra formulas or geometry directly, it strengthens essential problem-solving habits: logical deduction, pattern recognition, and persistence. These are exactly the skills tested in Canadian math contests like Gauss, Pascal, Euclid, and AMC 8.
Core Thinking Skills in Sudoku and Math Contests
| Skill | Sudoku Example | Gauss Contest Example |
| Pattern Recognition | Spotting a missing number in a row | 2022 Q4: Sequence 3, 8, 13, 18 → next terms |
| Logical Deduction | Eliminating candidates to find the only valid choice | 2022 Q17: Letter arithmetic; 2021 Q19: Subtraction with digits |
| Spatial Reasoning | Understanding 3×3 box interactions | 2022 Q5: Dice faces; 2020 Q19: Cube with symbols |
| Symmetry & Geometry | Balanced placement in the grid | 2020 Q16: Shading for diagonal symmetry |
| Global Optimization | Ensuring the whole solution is consistent | 2021 Q25: 12×12×12 cube sum maximization |
Pattern Recognition in Sudoku and Gauss Problems
In Sudoku, players often start with easy wins: spotting rows or columns where only one number is missing.
- Sudoku Example: In this 4×4 puzzle, children learn to complete rows by recognizing which numbers are missing.

- Gauss 2022 Q4: Extend the sequence 3, 8, 13, 18 by noticing the common difference of +5.

- Connection: Both require finding hidden patterns and applying them systematically. This habit also supports ratio word problems and algebra sequences in contests.
Logical Deduction for Math Contest Preparation
Sudoku is a constraint puzzle: every row, column, and box must contain each number once.
- Sudoku Example: In a 6×6 puzzle, players must check all possibilities and eliminate incorrect numbers until one option remains.

- Gauss 2022 Q17: Solve a letter-digit arithmetic puzzle that adds to 2022.
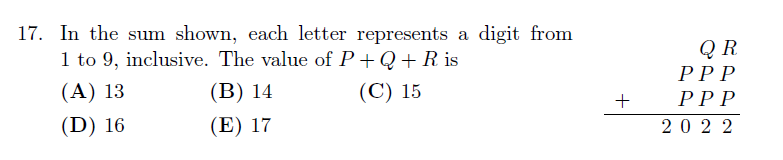
- Gauss 2021 Q19: Subtraction with digits (5□ – □5) requires testing and ruling out impossible results.

- Connection: These problems all demand step-by-step elimination. The same method is vital for algebra word problems and probability questions in contests like Pascal and Euclid.
Spatial Reasoning: From Sudoku Grids to Waterloo Cube Problems
Sudoku may be two-dimensional, but it demands spatial awareness across its 3×3 or 6×6 boxes.
- Gauss 2022 Q5: Deduce unseen dice faces using the “opposite sides sum to 7” rule.

- Gauss 2020 Q19: Reconstruct cube faces from multiple views.

- Connection: Both use partial information to rebuild a global structure, just like geometry word problems in Waterloo contests.
Symmetry and Geometry in Sudoku and Canadian Math Contests
Sudoku solutions often have symmetry, which players subconsciously use to predict placements.
- Gauss 2020 Q16: Shade squares so BD becomes a line of symmetry.
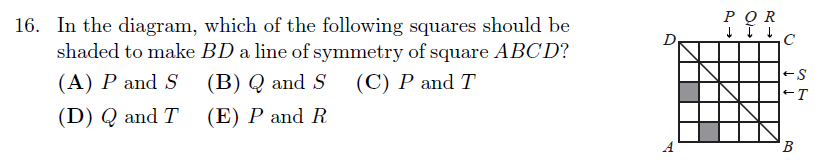
- Connection: This mirrors Sudoku’s reliance on structural balance. Geometric reasoning also appears in area and perimeter worksheets and geometry-focused contest problems.
Global Optimization: Sudoku and Large-Scale Contest Problems
A Sudoku solution must be valid globally: every part must work together.
- Gauss 2021 Q25: Arrange 1728 cubes in a 12×12×12 structure to maximize exterior sums.

- Connection: Both require global optimization, a strategy also useful in advanced Canadian math contests like Euclid and Fermat.
Practical Tips for Parents and Students
- Use Sudoku as a warm-up: 10–15 minutes before math practice gets the brain ready.
- Start simple: Move from 4×4 or 6×6 puzzles to harder versions, just like progressing from Pascal to Gauss to Euclid contests.
- Pair Sudoku with contest prep: Balance Sudoku with algebra word problems, ratio word problems, and probability practice, which are common in Canadian math contests.
- Keep it fun: Sudoku makes logical thinking engaging, supporting contest success in the long run.
Conclusion
So, can Sudoku help with math contest preparation? Yes—as a supplement. It cannot replace structured practice in algebra, geometry, or probability, but it builds the logical habits needed for the Waterloo Math Competition, and other Canadian math contests.
If your child enjoys Sudoku and Gauss puzzles, that curiosity is the perfect first step. To go further, structured programs can channel those skills into full contest readiness.
Next Step: Math Contest Preparation with Think Academy
At Think Academy CA, we build on puzzle-based logic like Sudoku and connect it to real contest strategies. Our programs cover:
- Step-by-step training for Gauss, Pascal, Euclid, and other Waterloo math contests.
- Core topics in algebra word problems, probability questions, geometry, and number theory.
- Guided practice with past contest questions and interactive problem-solving sessions.
- A supportive environment that helps students grow from fun puzzles to contest excellence.
Help your child turn their love of puzzles into real math contest skills. Learn more about our Think Academy Canada math contest courses and register for the free math evaluation.


