When parents think about math competition preparation, they often imagine advanced algebra or complicated geometry. But the truth is simpler: the foundation of success in contests like the AMC 8 or Gauss Contest is built on classic word problems strategies.
These problems—about boats, rabbits, or gardens—look like elementary school exercises. Yet they train the exact skills students need for contests: logical thinking, equation modeling, and systematic problem solving. In this article, we review 10 essential word problem types, show how they appear in school math, and explain how they connect directly to competition questions.
1. Ratio Word Problems in Math Contests
School Example (Q1): A class of 48 students goes boating, with 6 students per boat. Even after everyone boards, 7 boats are still empty. How many boats are there in total?

How to Solve: Divide 48 by 6 → 8 boats used. Add 7 empty → 15 total.
Why It Matters: This teaches students to model real-life sharing with division and addition. Ratio and fraction reasoning are cornerstones of contests.
Contest Example: 2020 AMC 8, Problem 5—three-fourths of a pitcher is poured evenly into 5 cups.
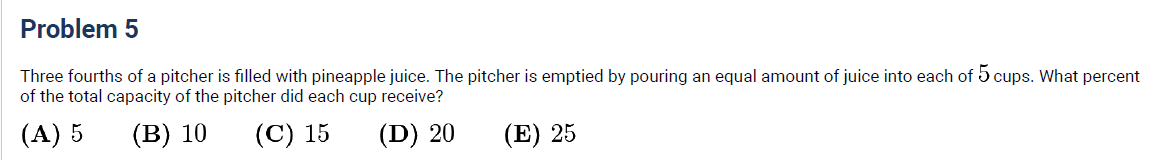
Each cup receives 15% of the pitcher’s capacity.
From equal sharing in school to ratio word problems with fractions and percentages in AMC 8, the skills are identical.
2. Queue and Sequence Word Problems
School Example (Q4): Alice is the 6th person from the front, Sara is the 5th from the back in a line of 15. How many people are between them?

How to Solve: Total – (Alice’s position + Sara’s position) + 1 = 15 – (6 + 5) + 1 = 5.
Why It Matters: Queue problems strengthen logical positioning and “number line” reasoning.
Contest Example: 2020 AMC 8, Problem 6—five people ride a small train. With conditions on who sits where, who is in the middle?

Queue problems evolve into logic-based word problems, exactly what AMC 8 and Gauss love to test.
3. Difference and Multiple Word Problems
School Example (Q7): Jenny has 48 books. Novels are 5 times the number of comic books.

How to Solve: Let comics = x, novels = 5x, total = 48 → 6x = 48 → x = 8 comics, 40 novels.
Why It Matters: This is a student’s first experience with setting up equations.
Contest Example: 2020 AMC 8, Problem 8—Ricardo has 2020 coins, some pennies and some nickels. What is the difference between the maximum and minimum possible values?

From simple “more than” relations to contest-level algebra word problems, students practice equation modeling at increasing difficulty.
4. Travel and Speed Word Problems
School Example (Q14): Linda drives 2 hours at 40 mph, then 3 hours at 70 mph. Find the total distance.

How to Solve: Distance = 2×40 + 3×70 = 80 + 210 = 290 miles.
Why It Matters: These problems connect rate, time, and distance—one of the most transferable math skills.
Contest Example: 2013 AMC 8, Problem 11—Grandfather walks different speeds on different days. If he had walked at one constant speed, how many minutes would he save?

Contests elevate distance-rate-time word problems from direct computation to conditional comparisons.
5. Age Word Problems
School Example (Q11): James is 12, his grandfather’s age is 5 times his. What was their age difference 4 years ago?

How to Solve: Grandfather = 60 now, James = 12. Difference always 48.
Why It Matters: Age problems teach students the idea of “invariants” (age difference stays constant) and dynamic ratios.
Contest Example: 2008 AMC 8, Problem 10
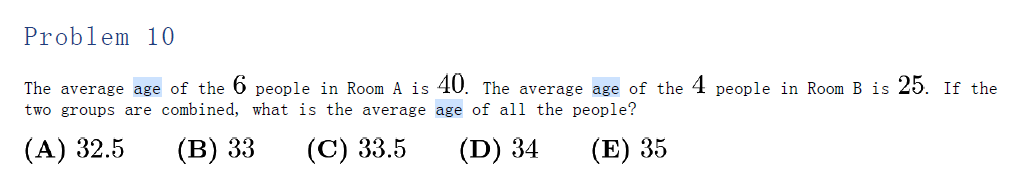
From simple subtraction to algebraic ratios in age problems, students practice reasoning about changing relationships.
6. Chicken and Rabbit Word Problems
School Example (Q13): A farm has 40 animals with 126 legs. How many are chickens and how many are rabbits?

How to Solve: Let chickens = x, rabbits = 40 – x. Then 2x + 4(40 – x) = 126 → x = 34 chickens, 6 rabbits.
Why It Matters: This is the most famous introduction to systems of equations.
Contest Example: 2018 Gauss, Problem 15
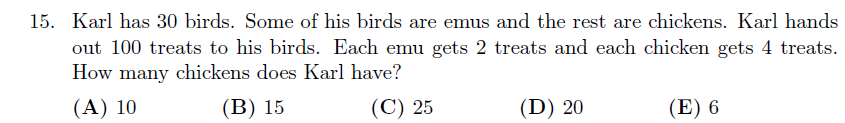
👉 From “chicken and rabbit” to multi-animal systems, this classic model grows into advanced algebra.
7. Calendar and Modular Word Problems
School Example (Q15): March 24, 2003 was Monday. What day was May 2, 2003?
How to Solve: Count days difference, divide by 7, take remainder.

Why It Matters: These problems introduce students to modular arithmetic, a core topic in number theory.
Contest Example: 2018 Gauss, Problem 14
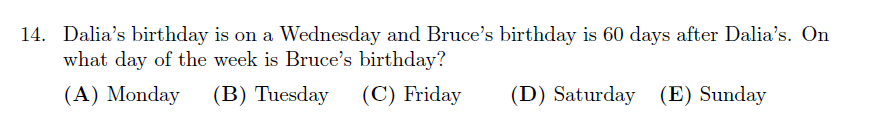
From weekly cycles to mod problems, calendar questions are early training for contest math.
8. Number Theory Word Problems
School Example (Q10, TAL course): Squary and Bubble Bubble compare pencils on a line segment graph. Students must see how one quantity can be expressed as “a multiple of another plus a remainder.”

Why It Matters: This is an early version of number theory reasoning. It introduces children to the idea that numbers can be broken into multiples and remainders—a key foundation for modular arithmetic and divisibility problems.
Contest Examples:
- 2013 AMC 8, Problem 10—ratio of LCM and GCF.

- 2013 AMC 8, Problem 13—digit reversal difference.

Why It Matters: These connect arithmetic, factors, and digit sense to contest-level integer word problems.
From divisibility in elementary school to AMC 8 factorization, number theory bridges daily math to contests.
9. Geometry Word Problems: Area and Perimeter
School Example: A rectangular garden is 8 meters long and 5 meters wide. What are its area and perimeter?
How to Solve:
- Area = length × width = 8 × 5 = 40 square meters.
- Perimeter = 2 × (length + width) = 2 × (8 + 5) = 26 meters.
Why It Matters:
Geometry problems connect visual reasoning with algebraic calculation. Students learn to apply formulas, but more importantly, they practice seeing how shapes and numbers interact. This spatial awareness becomes essential when the figures are no longer simple rectangles but more complex 2D or 3D structures in contests.
Contest Examples:
- 2020 AMC 8, Problem 9: A cube-shaped cake is cut into 64 smaller cubes. How many pieces have exactly two frosted faces?

From calculating the area of rectangles in elementary school to reasoning about 3D cube partitions in AMC 8, geometry word problems evolve into powerful exercises in spatial reasoning and problem solving.
10. Probability and Statistics Word Problems
Contest Example: 2010 AMC 8, Problem 12—500 balls, 80% red, remove how many red to leave 75% red?

How to Solve: Set up equation: (400 – x)/(500 – x) = 0.75 → x = 100.
Why It Matters: Probability teaches proportional reasoning and statistical thinking.
Practicing probability questions, mean median mode worksheets, and frequency tables prepares students for data-driven contest questions.
Final Thoughts: From Word Problems to Math Competition Success
Classic word problems are not random drills. They are the bridge from school math to AMC 8 practice and Gauss contests. Each type—whether ratio word problems, age word problems, geometry word problems, or probability questions—teaches students how to extract information, build equations, and solve systematically.
For parents and students serious about math competition preparation, mastering these ten categories is the first step.
Next Step: Take Think Academy’s free exam to practice these problems step by step, connect them to real AMC 8 and Gauss questions, and build the confidence to succeed in math competitions.


