Your Magic Key to Right Triangles!

Imagine this:
A ladder leans against a wall. The bottom is 3 steps from the wall. The top touches 4 steps high.
How long is the ladder?
The answer isn’t magic—it’s math! Meet the Pythagorean Theorem, a superpower for solving triangles.
What is the Pythagorean Theorem?
In any right-angled triangle (where one corner is a perfect 90° “L” shape), this rule always holds true:
The square of the longest side (hypotenuse) equals the sum of squares of the two shorter sides!
In math language:
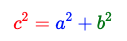
c = Hypotenuse (side opposite the right angle, always the longest!)
a and bb = Legs (the two sides that make the right angle)
Why Does It Work? Let’s Unlock the Secret!
Think like a puzzle master:
- Draw squares on each side of the triangle.
- The area of the square on cc always equals the sum of the areas on aa and bb!
https://www.mathsisfun.com/geometry/images/pythagoras-proof.svg
See how the blue + green squares fit perfectly into the red square? That’s the proof!
Try it yourself:

Super-Useful “Triples” to Know
Memorize these common right triangles – they’re time-savers!
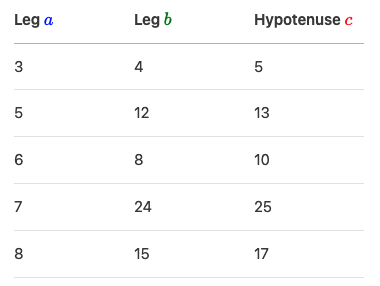
Fun Fact: If you multiply a triple (like 3-4-5) by 2, you get another triple: 6-8-10!
When and How to Use the Theorem
Got a right triangle? Need one missing side? Follow these steps:
- Label the sides: Find the legs (a, b) and hypotenuse (c).
- Write the equation: a2+b2=c2
- Plug in the numbers you know.
- Solve for the missing side!
Example:
A door is 4 feet wide and 7 feet tall. How long is its diagonal brace?
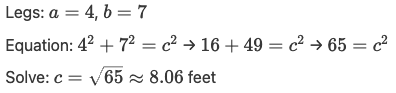
Watch Out for These Traps!

Why Pythagoras Rocks Math Competitions
- Solves sneaky geometry problems fast!
- Creates “aha!” moments with triples (like 5-12-13).
- Connects algebra and geometry – math supercombo!
- Builds logic skills for harder proofs.
Pro Tip: Practice spotting hidden right triangles in shapes like rectangles, diamonds, and even hexagons!
The Pythagorean Theorem isn’t just old history—it’s your secret weapon!
Master this tool, and you’ll slice through competition problems like a laser. Remember: Find the right angle, square the sides, add ’em up… and unlock the answer!
Challenge Yourself:
A TV screen is 30 inches wide and 40 inches tall. What’s the screen size (diagonal) in inches?
(Hint: Use a triple you know!)


