When preparing for the AMC 8, many students focus on algebra or geometry. However, one of the most frequently tested areas is number theory. Problems involving odd and even numbers, divisibility, prime factorization, and greatest common factor (GCF) or least common multiple (LCM) appear in almost every AMC 8 paper. In this guide, we will review 8 essential AMC 8 number theory formulas, connect each with a real AMC 8 problem, and explain how you can use integer worksheets and word problems practice to master these concepts.
1. Odd and Even
Formulas:

Example (AMC 8 2017 Problem 8):

A two-digit number satisfies three out of four conditions: prime, even, divisible by 7, contains the digit 9. Students must test parity first, then check divisibility and primality.
Why this matters:
Odd/even rules are the building blocks of AMC 8 word problems. Students who practice with integer worksheets that include adding and subtracting odd/even numbers can more easily see patterns during contest time.
2. Divisibility Rules for 2, 4, 8, 16, and 2ⁿ
Formulas:

Example (AMC 8 2018 Problem 7):
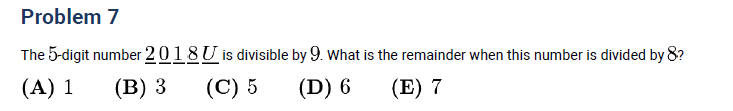
- First, apply digit-sum divisibility by 9.
- Then use the last-three-digits test for divisibility by 8.
Why this matters:
These divisibility rules are at the heart of many AMC 8 integer word problems. Parents can reinforce this at home with practice worksheets on factors and multiples, where students test divisibility by 2, 4, 8, and so on.
3. Divisibility Rules for 3 and 9
Formulas:

Example (AMC 8 2014 Problem 21):
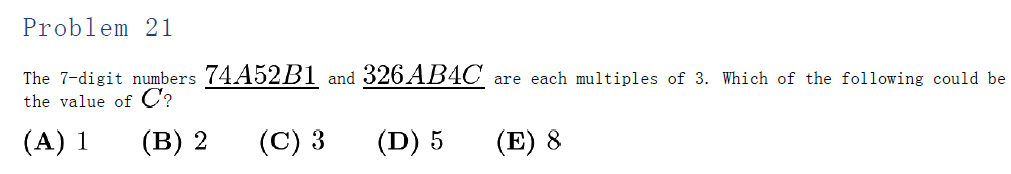
Two 7-digit numbers with missing digits must both be divisible by 3. The trick is applying digit-sum rules.
Why this matters:
These rules appear again and again in AMC 8 real problems. Students who practice with integer addition worksheets and digit-sum puzzles build strong pattern recognition for divisibility tests.
4. Divisibility Rules for 5, 25, 125, and 5ⁿ
Formulas:

Example (AMC 8 2014 Problem 2):
Paul must pay 35 cents using 5¢, 10¢, and 25¢ coins. What is the difference between the largest and smallest number of coins he could use?

Solution:
- Max coins: 7 nickels.
- Min coins: 25¢ + 10¢ = 2 coins.
- Difference = 5.
Why this matters:
Money problems are just disguised divisibility word problems. To prepare, students can use ratio word problems worksheets to connect real-life money calculations with divisibility concepts.
5. Divisibility Rule for 11
Formula:

Example (AMC 8 2017 Problem 7):

Six-digit numbers of the form abcabc‾\overline{abcabc}abcabc must be divisible by 1001 = 7 × 11 × 13. So 11 is always a factor.
Why this matters:
This type of problem teaches students to recognize repeating blocks in numbers. Teachers can prepare integer story problems that emphasize alternating digit sums to reinforce the 11-rule.
6. Divisibility Rules for 6, 12, 14, 15, 18, 24
Formulas:

Example (AMC 8 2018 Problem 21):
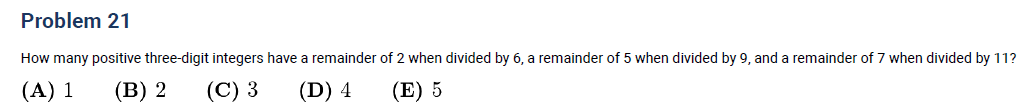
Find three-digit numbers that satisfy multiple remainders:
- remainder 2 mod 6,
- remainder 5 mod 9,
- remainder 7 mod 11.
This is a classic Chinese Remainder Theorem style problem, but students can solve step by step with divisibility rules.
Why this matters:
These are more advanced integer word problems. Students can build up confidence by solving ratio word problems and modular arithmetic practice worksheets before tackling AMC 8 level remainders.
7. Prime Factorization
Formulas:

Examples:

AMC 8 2016 Problem 9 → distinct prime factors of 2016.
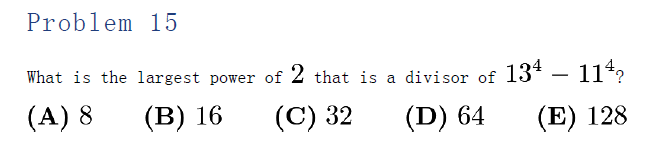
AMC 8 2016 Problem 15 → largest power of 2 dividing 134−11413^4-11^4134−114.

AMC 8 2018 Problem 14 → greatest 5-digit number with digit product 120.
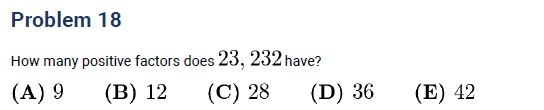
AMC 8 2018 Problem 18 → number of factors of 23,232.
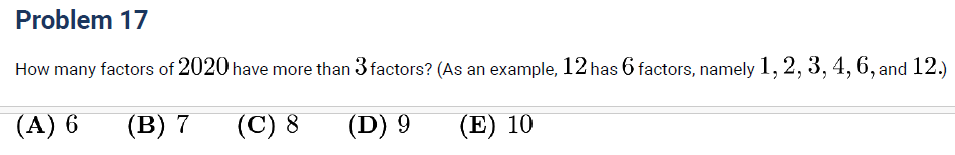
AMC 8 2020 Problem 17 → factors of 2020 with more than 3 factors.
Why this matters:
This is the core of AMC 8 number theory formulas. Students must be fluent in breaking numbers into primes. Teachers often assign dividing and multiplying integers worksheets to strengthen this skill.
8. GCF and LCM
Formulas:

Example (AMC 8 2012 Problem 15):

Find the smallest number greater than 2 that leaves remainder 2 when divided by 3, 4, 5, and 6.
- Number – 2 must be divisible by LCM(3,4,5,6) = 60.
- Answer: 62, which lies between 61 and 65.
Why this matters:
Many AMC 8 remainder problems depend on GCF and LCM. Students can use integer multiplication worksheets and practice sheets on multiples to get comfortable with LCM reasoning.
Final Thoughts
If your child is preparing for the AMC 8, focus on these 8 number theory formulas:
- Odd/even rules
- Divisibility rules (2,3,5,7,9,11…)
- Prime factorization
- GCF and LCM
Pairing each formula with real AMC 8 problems plus extra integer worksheets and ratio word problems gives students both accuracy and speed. This combination of formula mastery + contest practice is the most effective way to succeed in AMC 8 number theory.
Number theory is only one part of AMC 8 preparation. To fully build confidence, make sure to review our other guides: AMC 8 Counting and Probability Formulas, AMC 8 Algebra Formulas and AMC 8 Geometry Formulas. Together, these four resources cover the most important formulas, real AMC 8 problems, and practice strategies your child needs for contest success.
At Think Academy, we specialize in helping students master AMC 8 math through step-by-step teaching, interactive problem-solving, and targeted practice worksheets. If you want personalized guidance and a structured plan for AMC 8 success, book a free evaluation with Think Academy today.


