“An earthquake measuring 6.0 on the Richter scale is 10 times stronger than a 5.0 quake.”
“Canada’s population grew from 5 million to 38 million in 120 years – what’s the annual growth rate?”
These real-world mysteries are solved by logarithms – the indispensable inverse of exponents.

What Exactly Is a Logarithm?
Imagine exponents ask: “What is 2 raised to 3?” (Answer: 8).
Logarithms ask the reverse question: “2 raised to WHAT power gives 8?”
Mathematically:
If by=xby=x, then logb(x)=ylogb(x)=y
- Base (b): The “multiplier” (must be >0, ≠1)
- Argument (x): The result you start with
- Logarithm (y): The hidden exponent
Canadian Example:
106=1,000,000106=1,000,000 (a million) → log10(1,000,000)=6log10(1,000,000)=6
(Just like Toronto’s CN Tower is 553m tall – its height “exponent” relative to a 1m benchmark is log₁₀(553)≈2.74)
Logarithms vs. Exponents: Two Sides of the Same Coin
They undo each other like addition/subtraction:
| Operation | Example | Result |
|---|---|---|
| Exponentiation | 10³ | 1000 |
| Logarithm | log₁₀(1000) | 3 |

Key Insight:
blogb(x)=xblogb(x)=x and logb(bx)=xlogb(bx)=x
(Like converting Celsius to Fahrenheit and back)
Special Logarithm Types You’ll Meet
- Common Logarithm (Base 10)
- Written:log₁₀(x) or just log(x)
- Measures orders of magnitude:
- log₁₀(1,000)=3log₁₀(1,000)=3 (Canada has ~38M people → log₁₀(38,000,000)≈7.58)
- Used in: Richter scale, pH chemistry, decibels
- Natural Logarithm (Base e)
- Written: ln(x)ln(x)
- Base e≈2.71828e≈2.71828 (a fundamental constant like π)
- Models continuous growth/decay:
- Population dynamics (e.g., Alberta’s oil sands microbial growth)
- Radioactive decay (e.g., Saskatchewan’s uranium deposits)
Logarithm Laws: Your Math Toolkit
Master these rules to simplify complex problems:
1.Product Law
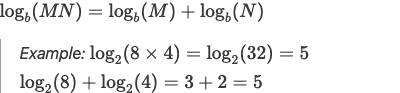
(Like combining BC and Alberta populations before calculating growth rate)
2.Quotient Law
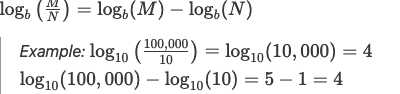
3.Power Law
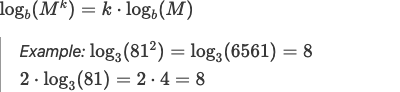
(Halving mortgage rates requires log calculations!)
4.Change of Base Formula
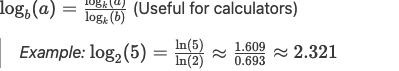
Why Logarithms Matter in Canada
- Finance: Calculating compound interest on TFSA/RRSP
- Geology: Dating rock layers using radioactive decay (e.g., Canadian Shield)
- Tech: Algorithm complexity (log N time in computer science)
- Ecology: Modeling boreal forest regeneration after wildfires
Fun Fact: Before calculators, engineers used slide rules – physical log scales – to build the CPR railway!
Logarithms transform multiplicative complexity into additive simplicity. From monitoring Vancouver Island earthquakes to predicting prairie crop yields, they turn exponential chaos into manageable calculations. Master the laws, practice with real data, and you’ll see why logs are the unsung heroes of STEM!
Visual Appendix:


